#2 O Princípio de Saint-Venant

Precisão VS Desempenho.

Essa é a saga de 100% das modelagens numéricas. Você quer ter resultados confiáveis, mas precisa atender os prazos que tem.

Por sorte, nem todos os detalhes realmente importam. O que nós queremos sempre é garantir um refinamento adequado dos detalhes (de geometria, malha, carregamentos e condições de contorno) na área que temos interesse e minimizar detalhes onde não temos.

Neste texto minha intenção é fazer uma breve explicação do princípio de Saint-Venant, que é a origem de algumas das principais técnicas de simplificação da modelagem. Se há algo fundamental para você compreender ao criar modelos numéricos, é ele.

Dica: nem sempre sabemos onde a região de concentração de tensão ou região de interesse está. Nessas situações minha sugestão é: teste! Faça uma rodada com poucos detalhes, malha grosseira e vá refinando.

O que é o princípio de Saint-Venant?

O entendimento dos estudos experimentais que originaram o princípio de Saint-Venant aconteceram ao longo dos anos, já que o artigo seminal data de 1855, com contribuição posterior inclusive do Richard von Mises, que foi assunto do primeiro texto.

Uma definição bem aceita é:

Sinceramente, esta definição por si só não diz muita coisa para mim.

Uma forma de entender, em outra palavras, é: se a sua zona de interesse não está imediatamente próxima da carga e/ou condição de contorno e/ou concentrador de tensão, essas coisas não vão ter influência significativa.

Mas por quê?

Porque é um princípio fundamental da mecânica que haja um equilíbrio das cargas estáticas, então por mais que o campo de tensão seja heterogêneo junto das regiões que citei acima, ele tende a se equilibrar (ficar homogêneo) em distância “suficiente”.

Muitos textos que li sobre o assunto trazem exemplos em chapas metálicas para ilustrar essa “homogeneização” das tensões, resolvi criar um exemplo um pouco mais intuitivo, fazendo um paralelo com tensões em uma chapa.

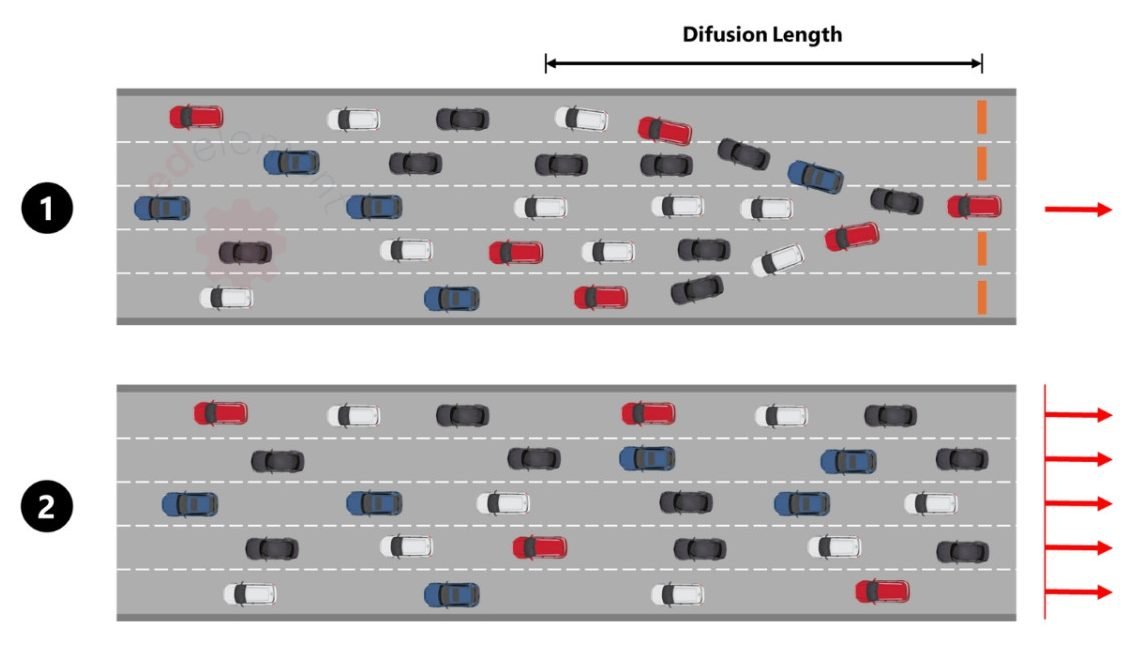
Na imagem abaixo, em 1, temos um engarrafamento (carga pontual/concentração de tensão), que leva a uma constrição (aumento de tensão local) e os carros ao passar por um bloqueio voltam a ocupar todas as faixas (homogeneização das tensões). Em 2, o efeito de todas as faixas abertas é análogo a uma carga distribuída.

A distância para essa zona de influência pode ser chamada de difusion length ou “comprimento de difusão”.

Nota: Retirei este termo do excelente webinar do Tony Abbey (NAFEMS) sobre o assunto. Recomendo a quem quiser se aprofundar.

Afinal, qual distância é “suficiente”?

A difusion length é uma ideia abstrata e não existe uma regra para essa distância da zona de influência local.

Duas coisas podem ditar essa distância:

• Detalhes geométricos. Por exemplo, 2 ou 3 vezes a distância da largura de uma barra.
• Experiência. Ao longo do tempo é comum criar esta noção.

Vamos a um exemplo simples.

Imagine que você quer analisar um quadro de bicicleta, sabe os carregamentos e a região de interesse.

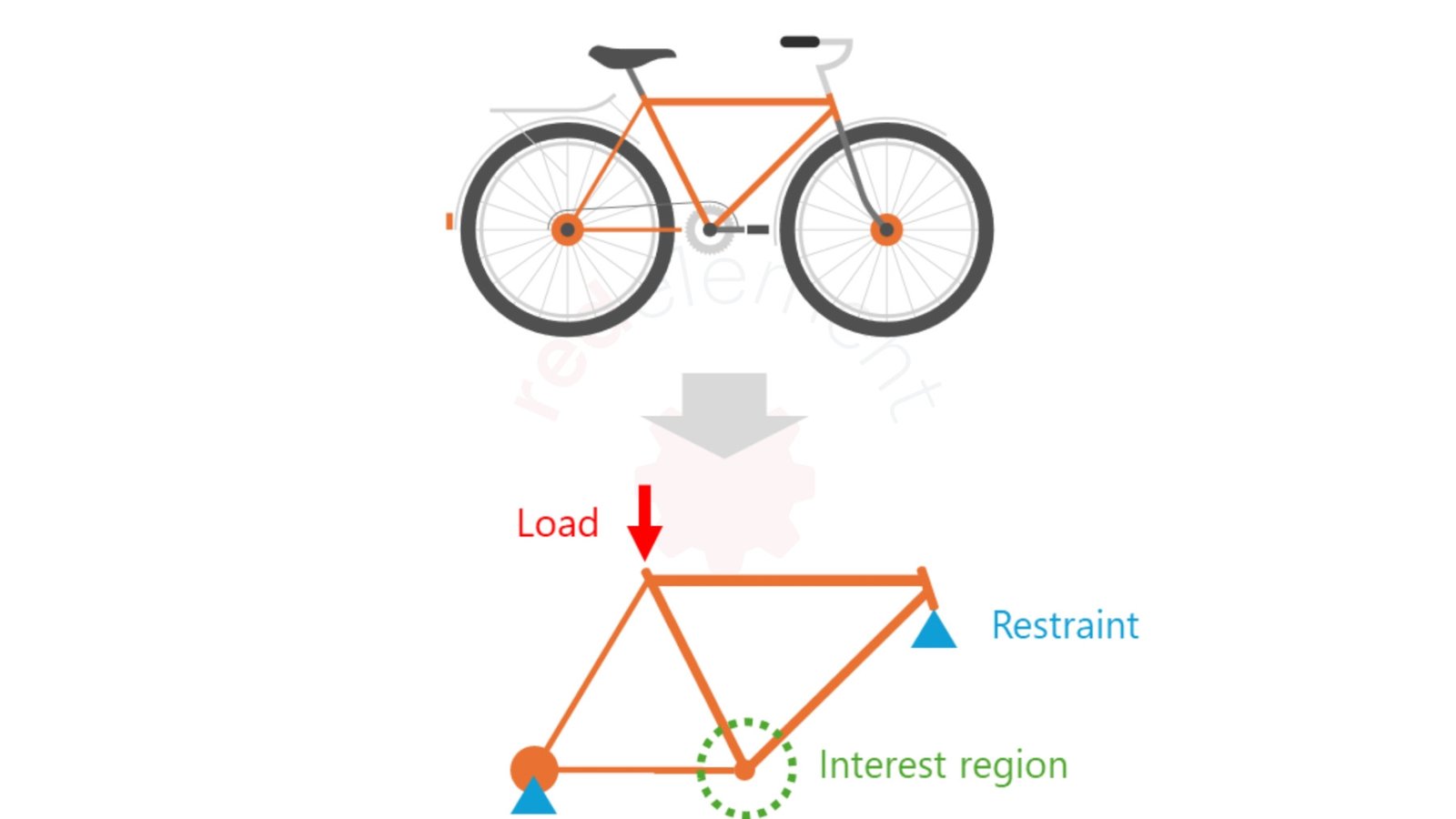
Cada elemento a mais na análise significa mais tempo de processamento. As vezes este tempo a mais é negligenciável e podemos arcar com um modelo mais pesado.

Mas imagine que você precisa fazer um estudo para encontrar a menor espessura possível para os tubos do quadro enquanto mantém a resistência necessária, e para isso você precisa analisar 10 espessuras diferentes.

Nessa situação este tempo se torna valioso.

Uma maneira de ter um modelo leve e rápido seria utilizando Saint-Venant e criando um submodelo, como na figura abaixo.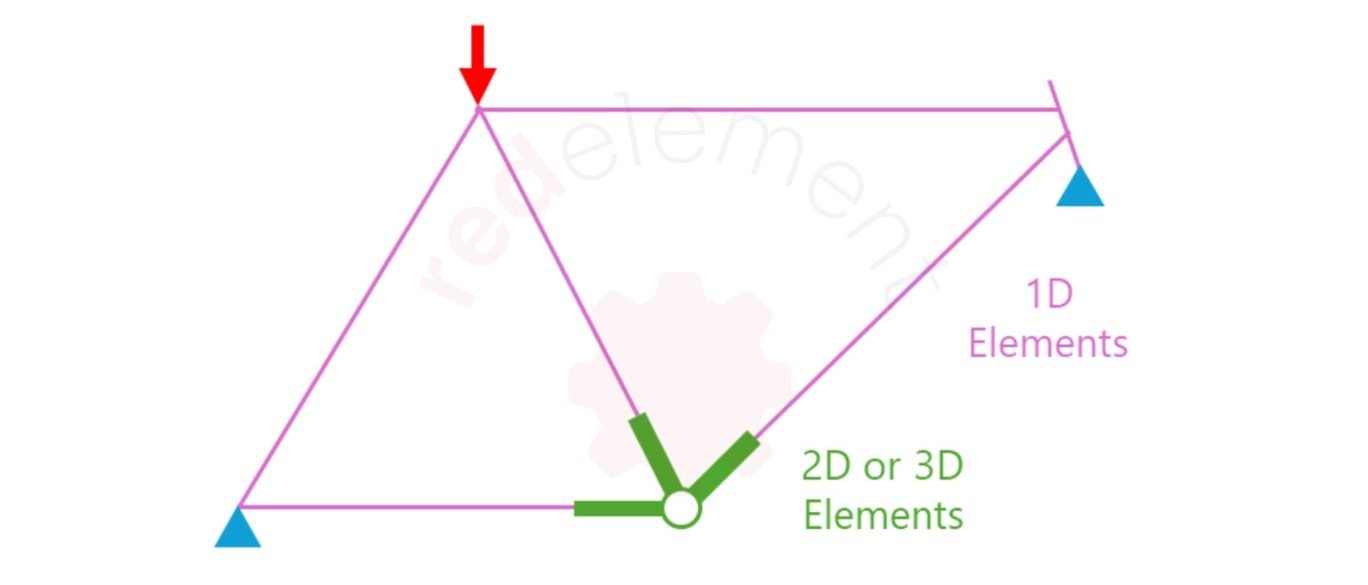 

Repare que todo o quadro foi simplificado com elementos 1D, também chamados de beams (vigas), que são computacionalmente muito mais leves.

A região de interesse do quadro pode ser modelada com elementos 2D ou 3D, dependendo do nível de detalhe desejado. Agora é possível se utilizar uma malha muito mais refinada e focar no que realmente importa.

Dica: para ligar os elementos 1D aos demais você pode usar elementos RBE2 ou RBE3.

Ao rodar a análise, a região de transição entre elementos 1D e 2D/3D concentrará tensão, mas se uma distância adequada foi deixada ela não deverá influenciar na área de interesse.

Foi dado um exemplo de submodelagem, mas preciso reforçar que este mesmo princípio pode ser aplicado, por exemplo, ao refinamento local de malha, simplificação de carregamentos e apoios, e tratamento de pontos com concentradores de tensão.

Realmente espero que algo tenha lhe sido útil neste texto!

Até a próxima,

Leandro Theodoro

Disclaimer sobre o uso de LLMs: Apesar do ChatGPT me ajudar muito na pesquisa sobre o tema e revisão, este texto é 100% escrito por mim e não gerado por um LLM.

Referências

1. 1. 1. (2022, January 10). Talking Shop with Tony Abbey – Episode 1 – St Venant’s Principle [Vídeo]. YouTube. https://www.youtube.com/watch?v=Fv23fkX0YhQ
      2. Wikipedia contributors. (n.d.). Saint-Venant’s principle. Wikipedia. Retrieved May 18, 2025, from https://en.wikipedia.org/wiki/Saint-Venant%27s_principle#:~:text=,sufficiently%20large%20distances%20from%20load
      3. von Mises, R. (1945). On Saint-Venant’s principle. Bulletin of the American Mathematical Society, 51(8), 555–562. https://www.ams.org/journals/bull/1945-51-08/S0002-9904-1945-08394-3/S0002-9904-1945-08394-3.pdf
      4. Engineering Stack Exchange contributors. (n.d.). What is Saint-Venant principle? Engineering Stack Exchange. Retrieved May 18, 2025, from https://engineering.stackexchange.com/questions/16666/what-is-saint-venant-principle